Radio de Curvatura de una Curva Regular

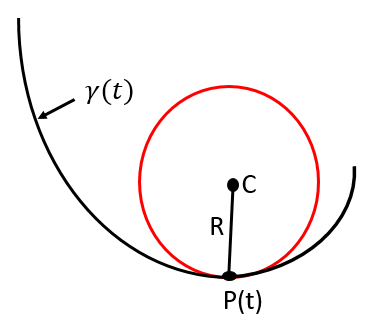
El radio de curvatura es una magnitud que nos permite calcular el radio de la circunferencia osculatriz en un punto t determinado o en punto s si la curva esta parametrizada en función de su longitud de arco ya sea en $R^2$ o en $R^n$ en el plano osculador correspondiente. 

El nombre de circunferencia osculatriz viene dado por que esta circunferencia es tangente a la curva respectivamente.

Circunferencia Osculatriz de radio R

Radio de Curvatura en Coordenadas Paramétricas

Para una curva plana en $R^2$ $\gamma(t) = (x(t), y(t))$, siendo t un parámetro arbitrario demostrar que su radio de curvatura es igual a la siguiente ecuación:

$$ {\Large \begin{equation*} R = \frac{[(\frac{dx}{dt})^2 + (\frac{dy}{dt})^2]^\frac{3}{2}}{\|\frac{dx}{dt}\frac{d^2y}{dt^2} - \frac{dy}{dt}\frac{d^2x}{dt^2}\|}\end{equation*}} $$

Demostración

 

Por definición de curvatura tenemos la siguiente ecuación

$$ {\large \begin{equation*} k = \left\| \frac{dT}{ds} \right \| \end{equation*}} $$

Ahora partiendo de la definición de vector unitario tangente.

$${\large \begin{align*} T &= \frac{\frac{d\gamma}{dt}}{\left\|\frac{d\gamma}{dt} \right\|} \\ T \left\|\frac{d\gamma}{dt}\right\| &= \frac{d\gamma}{dt} \end{align*}} $$

Luego derivando con respecto a t ambos miembros de la ecuación 

$$ {\large \begin{equation*} T\frac{d(\|\frac{d\gamma}{dt}\|)}{dt} + \frac{dT}{dt}\left\|\frac{d\gamma}{dt}\right\| = \frac{d^2\gamma}{dt^2} \end{equation*}} $$

Por último multiplicamos vectorial mente por T a ambos miembros de la igualada.

$$ {\large \begin{equation*} (T \times T)\frac{d(\|\frac{d\gamma}{dt}\|)}{dt} + \left(\frac{dT}{dt} \times T \right) \left\|\frac{d\gamma}{dt}\right\| = \frac{d^2\gamma}{dt^2} \times T \end{equation*}} $$

Por consiguiente la igualdad quedaría de la siguiente forma: 

$$ {\large \begin{align*} \left\| \frac{d\gamma}{dt} \right\| \left\| \frac{dT}{dt} \right\| &= \frac{\frac{d^2\gamma}{dt^2} \times \frac{d\gamma}{dt}}{\|\frac{d\gamma}{dt}\|} \\ \left\| \frac{dT}{dt} \right\| &=  \frac{\frac{d^2\gamma}{dt^2} \times \frac{d\gamma}{dt}}{\|\frac{d\gamma}{dt}\|^2} \end{align*} } $$

Volviendo a la ecuación de la curvatura

$$ {\large \begin{equation*} k = \left\| \frac{dT}{ds} \right\| = \left\| \frac{dT}{dt}\frac{dt}{ds} \right\| \end{equation*}} $$

Reemplazando $\Large \frac{dT}{dt}$ en k

$$ {\Large \begin{equation*} k = \frac{\left\| \frac{d^2\gamma}{dt^2} \times \frac{d\gamma}{dt} \right \|}{\|\frac{d\gamma}{dt}\|^3} \end{equation*}} $$

Como el radio de curvatura es el inverso de la curvatura entonces

$$ {\Large \begin{equation*} R = \frac{\|\frac{d\gamma}{dt}\|^3}{ \left\| \frac{d^2\gamma}{dt^2} \times \frac{d\gamma}{dt} \right \| } \end{equation*}} $$

Como $\gamma (t)$ se encuentra en $R^2$ entonces la ecuación del radio de curvatura queda de la siguiente manera.

$$ {\Large \begin{equation*} R = \frac{[(\frac{dx}{dt})^2 + (\frac{dy}{dt})^2]^\frac{3}{2}}{\|\frac{dx}{dt}\frac{d^2y}{dt^2} - \frac{dy}{dt}\frac{d^2x}{dt^2}\|} \end{equation*}} $$

Radio de Curvatura en Coordenadas Cartesianas

Para una función cartesiana $f = y(x)$. Demostrar que su radio de curvatura es igual a la siguiente ecuación:

$$ {\Large \begin{equation*} R = \frac{[ 1 + (\frac{dy}{dx})^2]^\frac{3}{2}} {\| \frac{d^2y}{dx^2} \|} \end{equation*}} $$

Demostración

Relacionando las variables cartesianas y el parámetro t tenemos lo siguiente:

$$ {\large \begin{equation*} \left\{ \begin{array}{lcc} x = t \\ y = x(t) \end{array} \right. \hspace{1.2cm}...\hspace{0.2cm} (1) \end{equation*}} $$

¡Ahora obtenemos las primeras y segundas derivadas de la ecuación (1)

$$ {\Large \begin{align*} & \left\{ \begin{array}{lcc} \frac{dx}{dt} = 1 \\ \frac{dy}{dt} = \frac{dy}{dx} \end{array} \right. \hspace{1.2cm}...\hspace{0.2cm} (2) \\ \\ & \left\{ \begin{array}{lcc} \frac{d^2x}{dt^2} = 0 \\ \frac{d^2y}{dt^2} = \frac{d^2y}{dx^2} \end{array}\right. \hspace{1.2cm}...\hspace{0.2cm} (3) \end{align*}} $$

Reemplazando las ecuaciones (2) y (3) en la ecuación de radio de curvatura en coordenadas paramétricas.

$$ {\Large \begin{align*}R &= \frac{[(\frac{dx}{dt})^2 + (\frac{dy}{dt})^2]^\frac{3}{2}}{\|\frac{dx}{dt}\frac{d^2y}{dt^2} - \frac{dy}{dt}\frac{d^2x}{dt^2}\|} \\ R &= \frac{[ 1 + (\frac{dy}{dx})^2]^\frac{3}{2}}{\|\frac{d^2y}{dx^2} \|} \\ \end{align*}} $$

Radio de Curvatura en Coordenadas Polares

Para una función polar $f = \rho(\theta)$. Demostrar que su radio de curvatura es igual a la siguiente ecuación:

$$ {\Large \begin{equation*} R = \frac{[\rho^2 + (\frac{d\rho}{dt})^2]^\frac{3}{2}}       {\|\rho^2 + 2\left(\frac{d\rho}{dt}\right)^2 - \rho\frac{d^2\rho}{dt^2}\|} \end{equation*}} $$

Demostración

Partiendo de las relaciones entre las coordenadas cartesianas y las coordenadas polares 

$$ {\large \begin{equation*} \left\{ \begin{array}{lcc}  x = \rho \cos{\theta} \\ y = \rho \sin{\theta} \end{array} \right. \hspace{1.2cm}...\hspace{0.2cm} (4) \end{equation*}} $$

Ahora obtenemos las primeras y segundas derivadas de la ecuación (4)

$$ {\Large \begin{align*} & \left\{ \begin{array}{lcc} \frac{dx}{d\theta} = \frac{d\rho}{d\theta} \cos{\theta} - \rho \sin{\theta} \\ \frac{dy}{d\theta} = \frac{d\rho}{d\theta} \sin{\theta} + \rho \cos{\theta} \end{array} \right. \hspace{1.2cm}...\hspace{0.2cm} (5) \\ \\ & \left\{ \begin{array}{lcc}\frac{d^2x}{d\theta^2} = \frac{d^2\rho}{d\theta^2} \cos{\theta} - 2\frac{d\rho}{d\theta}\sin{\theta} -\rho \cos{\theta} \\ \frac{d^2y}{d\theta^2} = \frac{d^2\rho}{d\theta^2} \sin{\theta} +  2\frac{d\rho}{d\theta}\cos{\theta} - \rho \sin{\theta}\end{array} \right. \hspace{1.2cm}...\hspace{0.2cm} (6)  \end{align*} } $$

Reemplazando las ecuaciones (4) y (5) en la ecuación de radio de curvatura en coordenadas paramétricas.

$$ {\Large \begin{align*} R &= \frac{[(\frac{dx}{dt})^2 + (\frac{dy}{dt})^2]^\frac{3}{2}}{\|\frac{dx}{dt}\frac{d^2y}{dt^2} - \frac{dy}{dt}\frac{d^2x}{dt^2}\|} \\ R &= \frac{[(\frac{dx}{d\theta})^2 + (\frac{dy}{d\theta})^2]^\frac{3}{2}}{\|\frac{dx}{d\theta}\frac{d^2y}{d\theta^2} - \frac{dy}{d\theta}\frac{d^2x}{d\theta^2}\|} \\ R &= \frac{[\rho^2 + (\frac{d\rho}{d\theta})^2]^\frac{3}{2}}{\|\rho^2 + 2\left(\frac{d\rho}{d\theta}\right)^2 - \rho\frac{d^2\rho}{d\theta^2}\|} \end{align*} } $$

Centro de Curvatura

El centro de curvatura es el centro de la circunferencia osculatriz. Ese centro respectivo puede estar dado en función de la longitud de arco o en su defecto por el parámetro t. Tomando como referencia de la imagen del inicio de este articulo podemos deducirla

• Centro de Curvatura en función del parámetro t

$${\large \begin{align*} C &= P + R(t)\vec{N}(t) \\ C &= \gamma (t) + \frac{\| \gamma' (t) \|^3 }{\| \gamma' (t) \times \gamma'' (t) \|} \left( \frac{[\gamma' (t) \times \gamma'' (t)] \times \gamma' (t)}{ \| [\gamma' (t) \times \gamma'' (t)] \times \gamma' (t) \| } \right) \\ C &= \gamma (t) + \frac{\| \gamma' (t) \|^3 }{\| \gamma' (t) \times \gamma'' (t) \|} \left( \frac{[\gamma' (t) \times \gamma'' (t)] \times \gamma' (t)}{ \| \gamma' (t) \times \gamma'' (t) \| \| \gamma' (t) \| } \right) \\ C &= \gamma (t) + \frac{\| \gamma' (t) \|^3 }{\| \gamma' (t) \times \gamma'' (t) \|} \left( \frac{ \gamma''(t) \| \gamma' (t) \|^2 - \gamma '(t) [ \gamma'(t) \cdot \gamma''(t) ]   } { \| \gamma' (t) \times \gamma'' (t) \| \| \gamma' (t) \| } \right) \\  C &= \gamma (t) + \left( \frac{\| \gamma' (t) \|^4  }{\| \gamma' (t) \times \gamma'' (t) \|^2} \right) \gamma'' (t) - \left( \frac{\| \gamma' (t) \|^2 [ \gamma'(t) \cdot \gamma''(t) ]}{\| \gamma' (t) \times \gamma'' (t) \|^2} \right) \gamma'(t) \end{align*}  }$$

• Centro de Curvatura en función de la longitud de arco

$${\large \begin{align*} C &= P + R(s)\vec{N}(s) \\ C &= \gamma (s) + R^2(s)\frac{dT}{ds} \\ C &= \gamma (s) + \frac{1}{\|\frac{dT}{ds} \|^2}\frac{dT}{ds} \\ C &= \gamma (s) + \frac{\gamma''(s) }{\| \gamma''(s) \|^2} \end{align*} }$$

Circunferencia Osculatriz de la Cicloide y Evoluta de la Cicloide.