La serie de Fourier es una serie infinita convergente que converge a una función periódica de periodo T en un determinado intervalo. La serie de Fourier es utilizada para resolver ecuaciones diferenciales parciales como la ecuación de calor y analizar el espectro de frecuencias de una función periódica. La serie de Fourier puede también extenderse al espacio de los números complejos.
Coeficientes de la serie de Fourier:
- $$\begin{equation*} a_0 = \frac{2}{T} \int_{-T/2}^{T/2} \left ( f(x) \right) \mathrm{d}x \end{equation*}$$
- $$\begin{equation*} a_n = \frac{2}{T} \int_{-T/2}^{T/2} \left( f(x)\cos\left( \frac{2n\pi x}{T} \right) \right) \mathrm{d}x \end{equation*}$$
- $$\begin{equation*} b_n = \frac{2}{T} \int_{-T/2}^{T/2} \left( f(x) \sin\left( \frac{2n\pi x}{T} \right) \right) \mathrm{d}x \end{equation*}$$
La serie de fourier de f(x) es igual a :
\begin{equation*} f(x) = \frac{a_0}{2} + \sum_{n=1}^{\infty} \left[ a_n \cos\left( \frac{2n\pi x}{T} \right) + b_n \sin\left( \frac{2n\pi x}{T} \right) \right] \end{equation*}
Código fuente de la serie de Fourier en Matlab
clear all
clc
syms x n
T = input(' Ingrese el periodo de f(x): ')
g = input(' Ingrese la función f(x): ')
%Coeficentes de Fourier
a_0 = (2/T).*int(g,x,-T/2,T/2);
a_m = (2/T).*int(g.*cos((2.*n.*pi.*x)./T),x,-T/2,T/2);
b_m = (2/T).*int(g.*sin((2.*n.*pi.*x)./T),x,-T/2,T/2);
F = (a_m).*(cos((2.*n.*pi.*x)./T)) + (b_m).*(sin((2.*n.*pi.*x)./T));
Cn = symsum(F,n,1,10);
Fourier = Cn + (a_0)/2;
t = linspace(-T/2,T/2,100);
f = input('Ingrese f(x) en función de t: ');
fplot(Fourier, [-T/2 T/2], 'b', 'linewidth', 3);
hold on
plot(t, f, 'k', 'linewidth', 2);
grid on
xlim([-T/2 T/2])
ylim([min(f) max(f)])
xlabel('Eje X')
ylabel('Eje Y')
title('Serie de Fourier de f(x) para n = 10')
legend('Fourier', 'f(x)')
Aplicación del código fuente
- Función Onda Cuadrada:
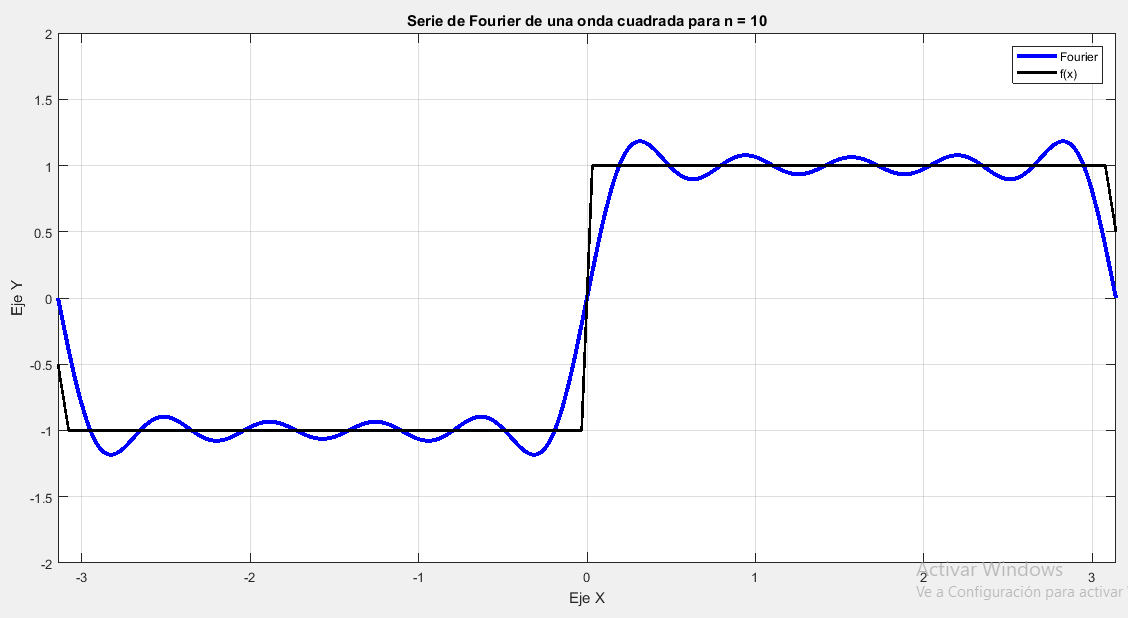 |
$$ \begin{equation*} f(x) = \left\{ \begin{array}{lcc} -x & si & -\pi < x < 0 \\ x & si & 0 < x < \pi \\ \end{array} \right. \end{equation*}$$ |
- Función Onda Diente de Sierra
 |
- Función de Onda Tren de Impulsos
 |
$$ \begin{equation*} f(x) = \left\{ \begin{array}{lcc} \sin{x} & si & 0 < x < \pi \\ 0 & si & \pi < x < 2\pi \end{array} \right. \end{equation*} $$ |
 |
$$ \begin{equation*} f(x)= \left\{ \begin{array}{lcc} \|\sin{x}\| & si & 0 < x < \pi \\ 0 & si & \pi < x < 2\pi \end{array} \right. \end{equation*}$$ |
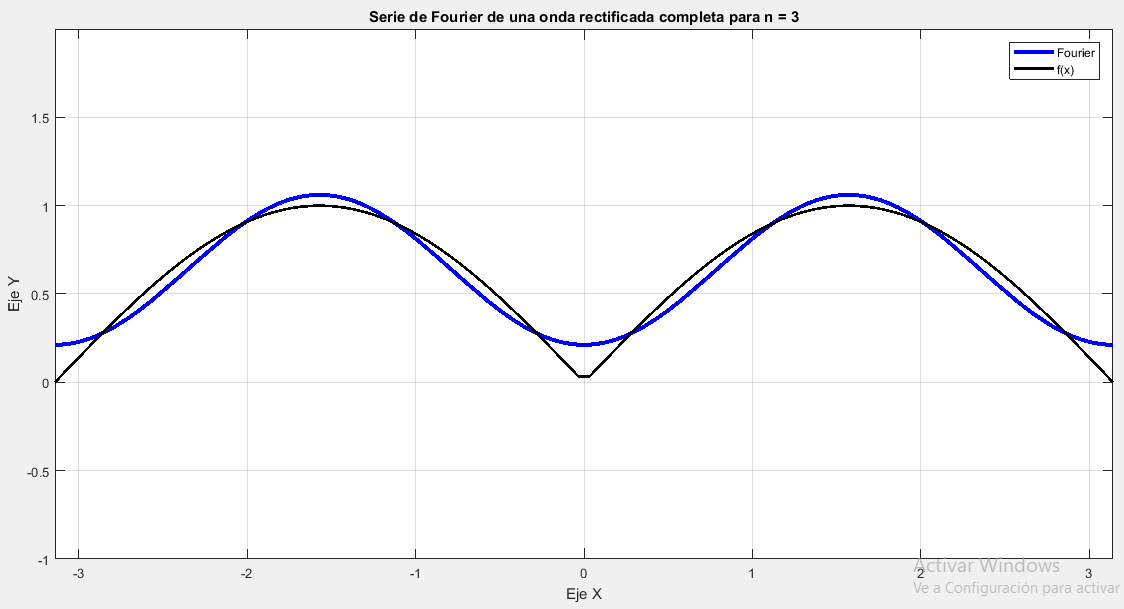 |

Comentarios
Publicar un comentario