Oscilador Armónico Cuántico Unidimensional

Haciendo uso de la ecuación de Schrondinger unidimensional independiente del tiempo

$${\large \begin{equation*} -\frac{\hbar ^2}{2m}\frac{d^2 \Psi}{dx^2} + V\Psi = E \Psi \hspace{1.5cm}...\hspace{0.2cm}(1) \end{equation*} }$$

La energía potencial de un oscilador armónico unidimensional sin rozamiento es igual a ${\large V = \frac{1}{2}Kx^2 }$. Por consiguiente reemplazando V en la ecuación (1) 

$${\large \begin{align*} -\frac{\hbar ^2}{2m}\frac{d^2\Psi}{dx^2} + V\Psi &= E \Psi \\ -\frac{\hbar ^2}{2m}\frac{d^2\Psi}{dx^2} + \frac{1}{2}Kx^2\Psi &= E \Psi \\ -\frac{\hbar ^2}{2m}\frac{d^2\Psi}{dx^2} + \left( \frac{1}{2}Kx^2 - E \right) \Psi &= 0 \hspace{1.5cm}...\hspace{0.2cm}(2) \end{align*} }$$

Si realizamos el cambio de variable ${\Large z = \beta x }$ respectivo obtenemos las siguientes relaciones siguientes:

$${\Large \begin{equation*}  \left\{ \begin{array}{lcc}              z = \beta x \hspace{1.8cm}...\hspace{0.2cm}(3) \\               \frac{d^2 \Psi}{dx^2} = \beta^2\frac{d^2 \Psi}{dz^2} \hspace{1.5cm}...\hspace{0.2cm}(4)             \end{array}   \right.  \end{equation*} }$$

Reemplazamos (3) y (4) en la EDO de la ecuación (2)

$${\large \begin{align*} -\frac{\hbar ^2}{2m}\frac{d^2\Psi}{dx^2} + \left( \frac{1}{2}Kx^2 - E \right) \Psi &= 0 \\ -\frac{\hbar ^2}{2m}\left(\beta^2 \frac{d^2\Psi}{dz^2} \right) + \left( \frac{1}{2}K\frac{z^2}{\beta^2} - E \right) \Psi &= 0 \\ \frac{\hbar ^2}{2m}\left(\beta^2 \frac{d^2\Psi}{dz^2} \right) - \left( \frac{Kz^2}{2\beta^2} - E \right) \Psi &= 0 \\ \beta^2 \frac{d^2\Psi}{dz^2} - \frac{m}{\hbar^2} \left( \frac{Kz^2}{\beta^2} - 2E \right) \Psi &= 0 \\ \frac{d^2\Psi}{dz^2} - \frac{m}{\hbar^2} \left( \frac{Kz^2}{\beta^4} - \frac{2E}{\beta^2} \right) \Psi &= 0 \hspace{1.5cm}...\hspace{0.2cm}(5) \end{align*} }$$

Si la constante ${\large \beta }$ es igual a ${\Large \left(\frac{\sqrt{mK}}{\hbar}\right)^{1/2} }$ entonces la EDO de la ecuación (5) toma la siguiente forma:

$${\large \begin{align*} \frac{d^2\Psi}{dz^2} - \frac{m}{\hbar^2} \left( \frac{Kz^2}{\beta^4} - \frac{2E}{\beta^2} \right) \Psi &= 0 \\ \frac{d^2\Psi}{dz^2} - \frac{m}{\hbar^2} \left(Kz^2 \frac{\hbar^2}{mK} - 2E\frac{\hbar}{\sqrt{mK}} \right) \Psi &= 0 \\ \frac{d^2\Psi}{dz^2} - \left(z^2 - \frac{2mE}{\hbar\sqrt{mK}} \right) \Psi &= 0 \hspace{1.5cm}...\hspace{0.2cm}(6) \end{align*} }$$

Si ${\Large \lambda = \frac{2mE}{\hbar\sqrt{mK}} }$ entonces la EDO de la ecuación (6) toma la forma siguiente:

$${\large \begin{align*} \frac{d^2\Psi}{dz^2} - \left(z^2 - \frac{2mE}{\hbar\sqrt{mK}} \right) \Psi &= 0 \\ \frac{d^2\Psi}{dz^2} - \left(z^2 - \lambda \right) \Psi &= 0 \hspace{1.5cm}...\hspace{0.2cm}(7) \end{align*} }$$

Si tomamos como solución de la EDO de la ecuación (7) la siguiente función y la reemplazamos después obtenemos

$${\large \begin{align*} \psi &= H(z) e^{- z^2 /2} \\ \frac{d\Psi}{dx} &= \left[ H'(z) - z H(z) \right]e^{- z^2 /2} \\ \frac{d^2 \Psi}{dx^2} &= \left[ H''(z) -2zH'(z) + H(z)\left( z^2 - 1 \right) \right]e^{- z^2 /2} \end{align*} }$$  

Por consiguiente: 

$${\Large \begin{align*} 0 &= H''(z) - 2zH'(z) + (\lambda - 1)H(z) \\ 0 &= H''(z) - 2zH'(z) + 2p H(z) \end{align*} }$$

La solución general de la ecuación diferencial de Hermite de orden p tiene una solución en serie de potencias, la cual es la siguiente.

$${\large \begin{align*} H(z) &= C_{0}\left[ 1 + \sum_{n=1}^{\infty}\left[ \frac{2^n \prod_{n=1}^{m}[2(m-1) - p]}{\Gamma[2n + 1]} \right]z^{2n} \right] \\ &+ C_{1}\left[ z + \sum_{n=1}^{\infty}\left[ \frac{2^n \prod_{n=1}^{m}[2m - 1 - p]}{\Gamma[2(n + 1)]} \right]z^{2n + 1} \right] \end{align*} }$$

Donde las soluciones aceptadas para que H(z) no diverja hacia el infinito son los polinomios físicos de Hermite. Los cuales estan dados por la siguiente ecuación.

$${\large \begin{equation*} H_{p}(z) = (-1)^p  e^{z^2}  \frac{d^{p} }{dz^{p}}\left( e^{-{z^2}} \right) \end{equation*} }$$

Los primeros polinomios físicos de Hermite son los siguientes

Orden p	Polinomio físico de Hermite grado p
0	$H_{0}(z) = 1$
1	$H_{1}(z) = 2z$
2	$H_{2}(z) = 4z^2 - 2$
3	$H_{3}(z) = 8z^3 - 12z$
4	$H_{4}(z) = 16z^4 - 48z^2 + 12$
5	$H_{5}(z) = 32z^5 - 160z^3 +120z$
6	$H_{6}(z) = 64z^6 - 480z^4 + 720z^2 - 120$
7	$H_{7}(z) = 128z^7 - 1344z^5 + 330z^3 - 1680z$
8	$H_{8}(z) = 256z^8 - 3584z^6 + 13440z^4 - 13440z^2 + 1680$
9	$H_{9}(x) = 512z^9 - 9216z^7 + 48384z^5 - 80640z^3 + 30240z$
10	$H_{10}(x) = 1024z^{10} - 23040z^8 + 161280z^6 - 403200z^4 + 302400z^2 -30240$

Por lo tanto la solución general del oscilador armónico cuántico unidimensional es la siguiente ecuación:

$${\large \begin{align*} \Psi(z) = C_{p}H_{p}(z) e^{-{z^2}/2} \\ \Psi(x) = C_{p}H_{p}(\beta x) e^{-{{(\beta x)}^{2}}/2} \end{align*} }$$

Donde: 

${\large C_{p}}$ es una constante de normalización respectiva. 

${\large \beta}$ es una constante igual a ${\large \left( \frac{mw}{\hbar} \right)^{1/2} }$

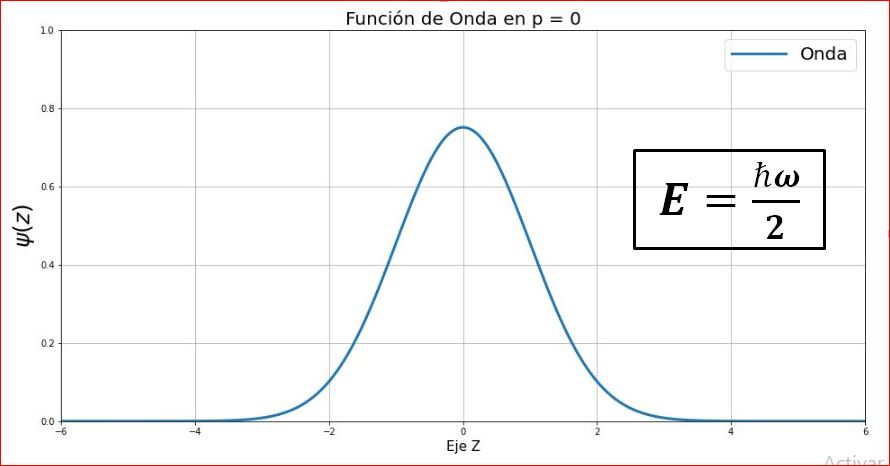
• Para p = 0

La constante de normalización es igual a ${\large C_{0}} ={\Large \frac{\sqrt{\beta}}{{\pi}^{1/4}}}$ y la funión de onda es la siguiente:

$${\Large \begin{equation*} \Psi(z) = \frac{e^{-{z^2}/2}}{{\pi}^{1/4}} \hspace{1cm},\hspace{1cm} \Psi(x) = \frac{\sqrt{\beta}e^{-\frac{\beta^2x^2}{2}}}{{\pi}^{1/4}} \end{equation*}}$$

Oscilador Armónico Cuántico Unidimensional en p = 0

• Para p = 1

La constante de normalización es igual a ${\large C_{1}} = {\Large \frac{\sqrt{\beta}}{\sqrt{2}{\pi}^{1/4}}}$ y la función de onda es la siguiente:

$${\Large \begin{equation*} \Psi(z) = \frac{\sqrt{2}ze^{-{z^2}/2}}{{\pi}^{1/4}} \hspace{1cm},\hspace{1cm} \Psi(x) = \frac{\sqrt{2}\sqrt{\beta}(\beta x)e^{-\frac{\beta^2x^2}{2}}}{{\pi}^{1/4}} \end{equation*}}$$

Oscilador Armónico Cuántico Unidimensional en p = 1

• Para p = 2

La constante de normalización es igual a ${\large C_{2}} = {\Large \frac{\sqrt{\beta}}{2\sqrt{2}{\pi}^{1/4}}}$ y la función de onda es la siguiente:

$${\Large \begin{equation*} \Psi(z) = \frac{(2z^2 - 1)e^{-{z^2}/2}}{\sqrt{2}{\pi}^{1/4}} \hspace{1cm},\hspace{1cm} \Psi(x) = \frac{\sqrt{\beta}(\beta^2 x^2 - 1)e^{-\frac{\beta^2 x^2}{2}}}{\sqrt{2}{\pi}^{1/4}} \end{equation*}}$$

Oscilador Armónico Cuántico Unidimensional en p = 2

Las funciones de onda del oscilador armónico cuántico unidimensional pueden hallarse partiendo de la propiedad de ortogonalidad de los polinomios físicos de Hermite.

$${\large \begin{align*} 1 &= \int_{-\infty}^{\infty} \left( \| \Psi(z)  \|^2 \right)dz \\ 1 &= \int_{-\infty}^{\infty} \left( ( C_{p}H_{p}(z) e^{-z^{2}/2})^2 \right)dz \\ 1 &= \int_{-\infty}^{\infty} \left( C_{p}^{2} H_{p}^{2}(z)e^{-z^2}\right)dz \\ 1 &=  \int_{-\infty}^{\infty} \left( C_{p}^{2} H_{p}^{2}(\beta x)e^{-\beta^2x^2}\right) dx \hspace{2cm}...\hspace{0.2cm}(8)  \end{align*} }$$

Los polinomios físicos de Hermite tienen la siguiente propiedad de ortogonalidad.

$${\large \begin{align*} 2^{p}(p!)\sqrt{\pi}\delta_{pq} &= \int_{-\infty}^{\infty} \left(  H_{p}(z)H_{q}(z)e^{-z^2} \right)dz \\ 2^{p}(p!)\sqrt{\pi}\delta_{pp} &= \int_{-\infty}^{\infty} \left(  H_{p}(z)H_{p}(z)e^{-z^2} \right)dz \\ 2^{p}(p!)\sqrt{\pi} &= \int_{-\infty}^{\infty} \left(  H_{p}^{2}(z)e^{-z^2} \right)dz \\  2^{p}(p!)\sqrt{\pi} &= \beta \int_{-\infty}^{\infty} \left(  H_{p}^{2}(\beta x)e^{-\beta^2 x^2} \right)dx \\ \frac{2^{p}(p!)\sqrt{\pi}}{\beta}  &= \int_{-\infty}^{\infty} \left(  H_{p}^{2}(\beta x)e^{-\beta^2 x^2} \right)dx \hspace{2cm}...\hspace{0.2cm}(9) \end{align*} }$$

Reemplazando (9) en la ecuación (8)

$${\large \begin{align*} 1 &= \int_{-\infty}^{\infty} \left( C_{p}^{2} H_{p}^{2}(\beta x) e^{-\beta^2x^2} \right) dx \\ 1 &=  C_{p}^{2} \int_{-\infty}^{\infty} \left( H_{p}^{2}(\beta x)e^{-\beta^2 x^2} \right)dx \\ 1 &= \frac{C_{p}^2 2^{p}p!\sqrt{\pi} }{\beta} \\ C_{p}^{2} &= \frac{\beta}{2^{p}p!\sqrt{\pi}} \\ C_{p} &= \sqrt{\frac{\beta}{2^{p}p!\sqrt{\pi}}} \end{align*} }$$

Por lo tanto la solución general del oscilador armónico cuántico unidimensional es igual a la siguiente ecuación:

$${\Large \begin{align*} \Psi(z) &= C_{p} H_{p}(z) e^{-z^{2}/2} \\ \Psi(x) &= C_{p} H_{p}(\beta x) e^{-\frac{\beta^2 x^2}{2}} \\ \Psi(x) &= \sqrt{\frac{\beta}{2^{p}p!\sqrt{\pi}}}\left( H_{p}(\beta x)e^{-\frac{\beta^2 x^2}{2}} \right) \end{align*} }$$

Donde: 

${\Large \beta}$ es una constante igual a ${\Large \left( \frac{mw}{\hbar} \right)^{1/2} }$