El Problema de la Braquistócrona

El problema de a braquistócrona fue uno de los problemas abiertos en el siglo XVII en el cuál se buscaba encontrar la curva en la cual el tiempo de descenso por acción de la fuerza de gravedad es mínimo.

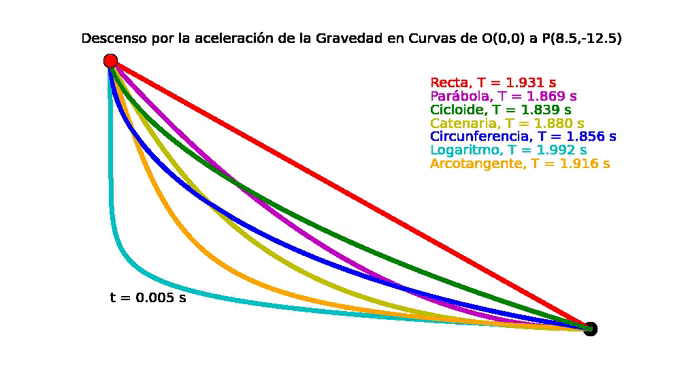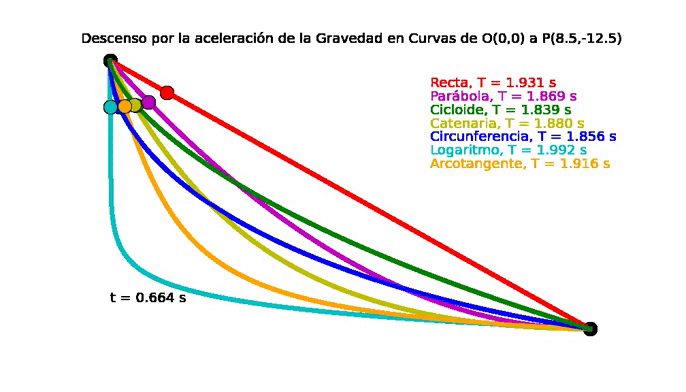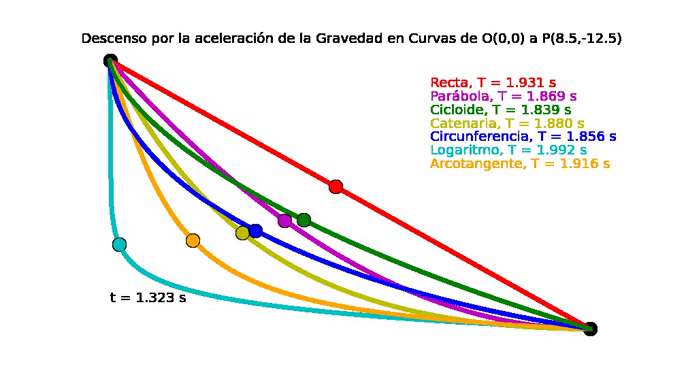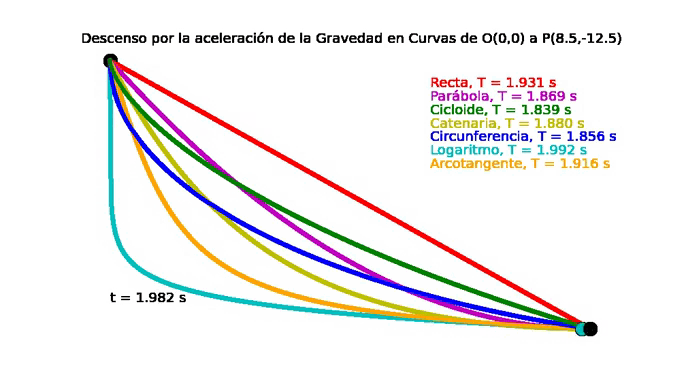
El problema de la braquistócrona para 7 curvas diferentes.

Curva en la cual el tiempo de descenso por acción de la fuerza de gravedad es mínimo.

Por el principio de conservación de la energía mecánica.

$$ {\large \begin{align*} E_{k} &= -U_{g} \\ \frac{mv^2}{2} &= mgy \\ v &= \sqrt{2gy} \hspace{1.5cm}...\hspace{0.2cm}(1) \end{align*}} $$

Por la longitud de arco para una función y = f(x)

$$ {\large \begin{align*}s &= \sqrt{1 + {y'}^2} \\ ds &= \sqrt{1 +  {y'}^2 }dx \hspace{1.5cm}...\hspace{0.2cm}(2) \end{align*}} $$

Por velocidad 

$$ {\large \begin{align*} v = \frac{ds}{dt} \hspace{1.5cm}...\hspace{0.2cm}(3) \end{align*}} $$

Reemplazando las ecuaciones (1) y (2) en la ecuación (3)

$$ {\large \begin{align*} v &= \frac{ds}{dt} \\ dt &= \frac{ds}{v} \\  dt &= \left( \frac{\sqrt{1+ {y'}^2}}{\sqrt{2gy}}\right) dx \\  t &= \int \left( \sqrt{\frac{1 + {y'}^2}{2gy}} \right) dx \\  t &= \frac{1}{\sqrt{2g}} \int \left( \sqrt{\frac{1 + {y'}^2}{y}}  \right) dx \hspace{1.5cm}...\hspace{0.2cm}(4) \end{align*}} $$

Siendo $ F = {\Large \sqrt{\frac{1 + {y'}^2}{y}} }$ el Lagrangiano del sistema. Por consiguiente usando la mecánica Lagrangiana obtenemos la ecuación de la curva.

$$ {\large \begin{align*} 0 &= \frac{\partial F}{\partial y} - \frac{\partial}{\partial t}\left( \frac{\partial F}{\partial y'} \right) \\ 0 &= \frac{\partial F}{\partial x} - \frac{\partial}{\partial x}\left( F - \frac{\partial F}{\partial y'} y' \right) \end{align*}} $$ Partiendo de la segunda ecuación de la mecánica Lagrangiana.

$$ {\large \begin{equation*} \frac{\partial F}{\partial x} - \frac{\partial}{\partial x} \left( F - \frac{\partial F}{\partial y'} y' \right)  = \left\{ \begin{array}{lcc} \frac{\partial F}{\partial x} = 0 &  \\ \\ F - \frac{\partial F}{\partial y'} y'  = K & \\ \end{array} \right. \hspace{1.5cm}...\hspace{0.2cm}(5)    \end{equation*}} $$

Partiendo de la ecuación (5) 

$$ {\large \begin{align*} K &= F - \frac{\partial F}{\partial y'} y' \\ K &= \frac{\sqrt{1 + {y'}^2}}{\sqrt{y}} - \frac{y'}{\sqrt{y}}\left( \frac{y'}{\sqrt{1 + {y'}^2 }} \right) \\ \sqrt{y}K &= \sqrt{1 + {y'}^2} - \frac{{y'}^2}{\sqrt{1 + {y'}^2}} \\ 1 &= \sqrt{y}K\sqrt{1 + {y'}^2} \\ 1 + {y'}^2 &= \frac{1}{K^2 y} \\ \frac{dy}{dx} &= \sqrt{\frac{1 - K^2 y}{K^2 y}} \\ \frac{dx}{dy} &= \sqrt{\frac{K^2 y}{1 - K^2 y}} \hspace{1.5cm}...\hspace{0.2cm}(6) \end{align*}} $$

Haciendo un cambio de variable $z = \sqrt{y}$ en la ecuación (6) 

$$ {\large \begin{align*} \frac{dx}{dy} &= \sqrt{\frac{K^2 y}{1 - K^2 y}} \\ \frac{dx}{dz} &= \frac{2Kz^2}{\sqrt{1 - K^2 z^2}} \hspace{1.5cm}...\hspace{0.2cm}(7) \end{align*}} $$ 

Haciendo una sustitución trigonométrica en la ecuación (7)

$$ {\large \begin{align*}  Kz &= \sin{\theta} \\ Kdz &= \cos{\theta}d\theta \end{align*}} $$

Por consiguiente

$$ {\large \begin{align*} \frac{dx}{dz} &= \frac{2Kz^2}{\sqrt{1 - K^2 z^2}} \\ x &= \int \left( \frac{2Kz^2}{\sqrt{1 - K^2 z^2}} \right)dz \\ x &= \int \left( \frac{2K\sin^2{\theta}\cos{\theta}}{K^3 \cos{\theta}} \right)d\theta \\ x &= \frac{2}{K^2} \int ( \sin^2{\theta} ) d\theta \\ x &= \frac{2}{K^2} \int \left( \frac{1 - \cos{2\theta}}{2} \right)d\theta \\ x &= \frac{1}{2K^2} \left( 2\theta - \sin{2\theta} \right) + C_{1} \hspace{1cm},\hspace{0.3cm} x = 0  \\ x &= \frac{1}{2K^2} \left( 2\theta - \sin{2\theta} \right) \end{align*}} $$

Partiendo de la relación trigonométrica $ Kz = \sin{\theta} $ del triangulo anterior

$$ {\large \begin{align*} Kz &= \sin{\theta} \\ K(\sqrt{y}) &= \sin{\theta} \\ K^2 y &= \sin^2{\theta} \\ y &= \frac{1}{2K^2}\left( 1 - \cos{2\theta} \right) \end{align*}} $$

Por lo tanto la ecuación de la curva $\gamma (\theta)$ en la cual el tiempo de descenso por acción de la fuerza de gravedad es mínimo es la siguiente.

$$ {\large \begin{equation*} \gamma (\theta)  = \left\{ \begin{array}{lcc} x(\theta) = \frac{1}{2K^2} \left( 2\theta - \sin{2\theta} \right) \\ \\ y(\theta) = \frac{1}{2K^2}\left( 1 - \cos{2\theta} \right)  \\ \end{array} \right. \end{equation*}} $$

Si realizamos un cambio de variable.

$$ {\large \begin{equation*} r = \frac{1}{2K^2} \hspace{1.5cm},\hspace{1.5cm} \varphi = 2\theta  \end{equation*}} $$

Entonces la curva que se obtiene es una cicloide.

$$ {\large \begin{equation*} \gamma (\varphi)  = \left\{ \begin{array}{lcc}  x(\varphi) = r \left( \varphi - \sin{\varphi} \right) \\ \\  y(\varphi) = r \left( 1 - \cos{\varphi} \right)  \\ \end{array} \right.\end{equation*}} $$

Donde ${\large \varphi = [0, 2\pi] }$

Construcción de la Cicloide

Propiedad Braquistócrona de la Cicloide: Tiempo mínimo de descenso por acción de la fuerza de gravedad.

Partiendo de la ecuación de la cicloide

$$ {\large \begin{align*} \gamma (\varphi) &= \left\{ \begin{array}{lcc} x(\varphi) = r \left( \varphi - \sin{\varphi} \right) &,&  \varphi = [0, 2\pi] \\ \\  y(\varphi) = r \left( 1 - \cos{\varphi} \right) &,& \varphi = [0, 2\pi] \\ \end{array} \right. \end{align*}} $$

Los diferenciales de longitud son:

 

$$ {\large \begin{align*} dx &= r(1 - \cos{\varphi})d\varphi \\ dy &= r\sin{\varphi}d\varphi \end{align*}} $$

Por longitud de arco

$$ {\large \begin{align*} ds &= \sqrt{1 + {y'}^2}dx  \\ ds &= \sqrt{1 + \left(\frac{dy}{dx}\right)^2} dx \\ ds &= r\sqrt{1 + \left( \frac{r\sin{\varphi}}{r(1 -\cos{\varphi})}\right)^2} (1 - \cos{\varphi})d\varphi \\ ds &= 2r\sqrt{1 + \left( \frac{\sin{\varphi}}{2\sin^2{(\varphi/2)}}\right)^2} \left( \frac{1 - \cos{\varphi}}{2} \right)d\varphi \\ ds &= 2r\sin^2{(\varphi/2)}\sqrt{1 + \left( \frac{\cos{(\varphi/2)}}{\sin{(\varphi/2)}}\right)^2} d\varphi \\ ds &= 2r\sin^2{(\varphi/2)}\sqrt{1 + \cot^2{(\varphi/2)}}  d\varphi \\ ds &= 2r\sin^2{(\varphi/2)} \sqrt{\csc^2{(\varphi/2)}} d\varphi \\ ds &= 2r\sin^2{(\varphi/2)} \csc{(\varphi/2)} d\varphi \\ ds &= 2r\sin{(\varphi/2)} d\varphi \hspace{1.5cm}...\hspace{0.2cm}(8) \end{align*}} $$

Reemplazando (8) en la ecuación (4) e integrando desde 0 hasta $\pi$

$$ {\large \begin{align*} t &= \frac{1}{\sqrt{2g}} \int \left( \sqrt{\frac{1 + {y'}^2}{y}}  \right) dx \\  t &= \frac{1}{\sqrt{2g}} \int_{0}^{\pi} \left( \frac{ 2r\sin{(\varphi/2)} } {\sqrt{r(1 - \cos{\varphi})}}  \right) d\varphi \\ t &= \frac{1}{\sqrt{2g}} \int_{0}^{\pi} \left( \frac{ 2r\sin{(\varphi/2)} } { \sqrt{2r\sin^2{(\varphi/2)}}  }  \right) d\varphi \\ t &= \frac{1}{\sqrt{2g}} \int_{0}^{\pi} \left( \sqrt{2r}  \right) d\varphi \\ t &= \sqrt{\frac{r}{g}}\int_{0}^{\pi} d\varphi \\ t &= \pi \sqrt{\frac{r}{g}} \end{align*} } $$

Por lo tanto el tiempo mínimo de descenso por acción de la fuerza de gravedad es igual a ${\Large t = \pi \sqrt{\frac{r}{g}} }$

Propiedad Braquistócrona de la Cicloide

Propiedad del isocronismo de la Cicloide: La propiedad de la braquistócrona es independiente del punto de partida.

 Partiendo de la ecuación (4) e integrando desde $\alpha$ hasta $\pi$ 

$$ {\large \begin{align*} t &= \frac{1}{\sqrt{2g}} \int \left( \sqrt{\frac{1 + {y'}^2}{y - y_{0}}}  \right) dx \\ t &= \frac{1}{\sqrt{2g}} \int_{\alpha}^{\pi} \left( \frac{2r\sin{(\varphi/2)} }{\sqrt{r(1 - \cos{\varphi} - 1 + \cos{\alpha})}}  \right) d\varphi \\ t &= \frac{\sqrt2{r}}{\sqrt{2g}} \int_{\alpha}^{\pi} \left( \frac{\sin{(\varphi/2)} }{\sqrt{\cos{\alpha} -  \cos{\varphi})}}  \right) d\varphi \\ t &= \frac{\sqrt{r}}{\sqrt{2g}} \int_{\alpha}^{\pi} \left( \frac{ \sin{(\varphi/2)} }{\sqrt{2\cos^2{(\alpha/2)} - 1 - 2\cos^2{(\varphi/2)} + 1)}}  \right) d\varphi \\ t &= \frac{\sqrt{2r}}{\sqrt{2g}} \int_{\alpha}^{\pi} \left( \frac{ \sin{(\varphi/2)} }{\sqrt{\cos^2{(\alpha/2)} - \cos^2{(\varphi/2})}}  \right) d\varphi \\ t &= \sqrt{\frac{r}{g}} \int_{\alpha}^{\pi} \left( \frac{ \sin{(\varphi/2)} }{\sqrt{\cos^2{(\alpha/2)} - \cos^2{(\varphi/2})}}  \right) d\varphi  \end{align*}} $$

Si definimos b = $\cos{(\alpha/2)}$ entonces la ecuación del tiempo toma la forma

$$ {\large \begin{align*} t &= \sqrt{\frac{r}{g}} \int_{\alpha}^{\pi} \left( \frac{ \sin{(\varphi/2)} }{\sqrt{\cos^2{(\alpha/2)} - \cos^2{(\varphi/2})}}  \right) d\varphi \\ t &= \sqrt{\frac{r}{g}} \int_{\alpha}^{\pi} \left( \frac{ \sin{(\varphi/2)} }{\sqrt{ b^2 - \cos^2{(\varphi/2})}}  \right) d\varphi \hspace{1.5cm}...\hspace{0.2cm}(9) \end{align*}} $$

Haciendo una sustitución trigonométrica en la ecuación (9)

Por consiguiente 

$$ {\large \begin{align*} t &= \sqrt{\frac{r}{g}} \int_{\alpha}^{\pi} \left( \frac{ \sin{(\varphi/2)} }{\sqrt{ b^2 - \cos^2{(\varphi/2})}}  \right) d\varphi \\ t &= -2\sqrt{\frac{r}{g}}\int_{\pi/2}^{0} \left( \frac{ b\sin{(\varphi/2)}\cos{\beta} }{b\cos{\beta}\sin{(\varphi/2)}}  \right) d\beta \\ t &= -2\sqrt{\frac{r}{g}}\int_{\pi/2}^{0} d\beta \\ t &= -2\sqrt{\frac{r}{g}}\left(-\frac{\pi}{2} \right) \\ t &= \pi\sqrt{\frac{r}{g}} \end{align*}} $$

Por lo tanto el tiempo de descenso en una cicloide es independiente del punto de partida, es decir, un arco de cicloide también cumple la propiedad de la braquistócrona. 

Propiedad del Isocronismo en la Cicloide

La propiedad del isocronismo de la cicloide también puede usarse para hacer péndulos que oscilen en una cicloide respectivamente.

Péndulo de Huygens