El Péndulo es un sistema físico que puede oscilar bajo la acción gravitatoria u otra característica física (elasticidad, por ejemplo) y que está configurado por una masa suspendida de un punto o de un eje horizontal fijos mediante un hilo, una varilla u otro dispositivo que sirve para medir el tiempo.
 |
| DCL del péndulo simple |
Péndulo Simple para oscilaciones pequeñas
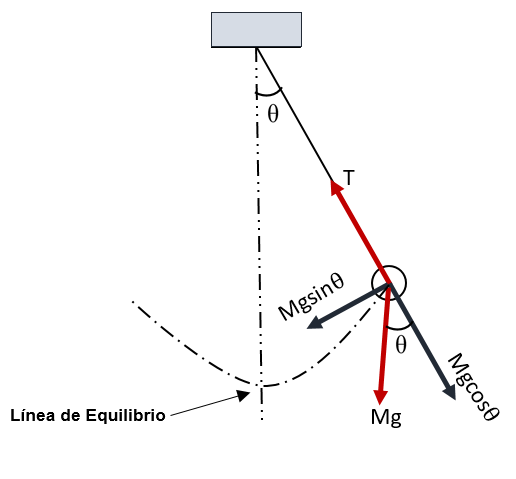
Un péndulo simpe es un sistema idealizado, es decir no existe en la realidad, sin embargo es útil para estudiar como un modelo teórico. El péndulo simple esta constituido por una partícula de masa m que está suspendida de un punto fijo o mediante un hilo inextensible con peso despreciable, se considera estas características para poder simplificar el problema. El movimiento del péndulo simple ocurre por una fuerza restauradora que siempre apunta hacia el punto de equilibrio, en este caso la fuerza restauradora es el peso de la partícula de masa m. El péndulo simple puede tratarse con las leyes de newton o con las ecuaciones de Lagrange.
 |
| Simulación de un péndulo simple lineal con un ángulo de $\theta = 15^{\circ}$ |
Por la Segunda Ley de Newton
$${\large \begin{align*}F &= ma \\-mgsin\theta &= m\frac{d^2r}{dt^2} \\ -gsin\theta &= L\frac{d\theta^2}{dt^2} \\ L\frac{d\theta^2}{dt^2} + gsin\theta &= 0\end{align*}}$$
Las oscilaciones de este péndulo oscila para ángulos $\theta$ menores de $\theta \leq 15^{\circ}$, entonces la ecuación diferencial toma la siguiente forma:
$${\large \begin{align*} L\frac{d\theta^2}{dt^2} + g\theta &= 0 \\ \frac{d\theta^2}{dt^2} + \frac{g\theta}{L} \end{align*}}$$
Ahora resolviendo esta ecuación diferencial de segundo orden homogénea por medio de la ecuación característica, nos da la siguiente solución.
$${\large \begin{equation*} \theta (t) = C_1 \cdot \cos\left(\sqrt{\frac{g}{L}}t\right) + C_2 \cdot \sin\left(\sqrt{\frac{g}{L}}t\right) \end{equation*}}$$
Ahora si deseamos saber el periodo respectivo del péndulo, simplemente recordando la dinámica de un movimiento circular podemos hallarla usando la frecuencia angular.
$${\large \begin{equation*} w = \frac{2\pi}{T} \end{equation*} }$$
La frecuencia angular es igual al argumento de la solución de la ecuación diferencial de segundo orden de a dinámica del péndulo, por consiguiente $ w = \sqrt{\frac{g}{L}} $, entonces reemplazando en la ecuación de la frecuencia angular tenemos:
$${\large \begin{align*} w &= \frac{2\pi}{T} \\ \sqrt{\frac{g}{L}} &= \frac{2\pi}{T} \\ T &= 2\pi \sqrt{\frac{L}{g}} \end{align*} }$$
Cinemática del péndulo simple para oscilaciones pequeñas
Conociendo la ecuación angular del péndulo simple
$${\large \begin{equation*} \theta (t) = C_1 \cdot \cos\left(\sqrt{\frac{g}{L}}t\right) + C_2 \cdot \sin\left(\sqrt{\frac{g}{L}}t\right) \end{equation*}}$$
Se puede encontrar su posición, velocidad y aceleración las cuales son las siguientes:
$${\large \begin{align*} r(t) &= L\left[ C_1 \cdot \cos\left(\sqrt{\frac{g}{L}}t\right) + C_2 \cdot \sin\left(\sqrt{\frac{g}{L}}t\right)\right] \\ v(t) &= L\left[C_2 \cdot \sqrt{\frac{g}{L}} \cdot \cos\left(\sqrt{\frac{g}{L}}t\right) - C_1 \cdot \sqrt{\frac{g}{L}} \sin\left(\sqrt{\frac{g}{L}}t\right)\right] \\ a(t) &= - L\left[ \frac{g\cdot C_1}{L} \cdot \cos\left(\sqrt{\frac{g}{L}}t\right) + \frac{g \cdot C_2}{L} \cdot \sin\left(\sqrt{\frac{g}{L}}t\right)\right] \end{align*} }$$
Estas ecuaciones del movimiento se pueden aún simplificar usando el siguiente artificio matemático de la suma de ángulos.
$${\large \begin{equation*} \sin{\left(\phi + \sqrt{\frac{g}{L}}t\right) } = C_1 \cdot \cos\left(\sqrt{\frac{g}{L}}t\right) + C_2 \cdot \sin\left(\sqrt{\frac{g}{L}}t\right) \end{equation*} }$$
donde:
- $\sin{\phi} = C_1$
- $\cos{\phi} = C_2$
- $ \arctan{\left( \frac{ C_1}{C_2} \right)} $
Por consiguiente si reemplazamos los datos obtenidos podemos transformar las anteriores ecuaciones en las siguientes.
$${\large \begin{align*} r(t) &= L \sin{\left( \sqrt{\frac{g}{L}}t + \arctan{\left( \frac{C_1}{C_2} \right )} \right) } \\ v(t) &= \sqrt{gL} \cdot \cos{\left( \sqrt{\frac{g}{L}}t + \arctan{\left( \frac{C_1}{C_2}\right)} \right) } \\ a(t) &= - g \cdot \sin{\left( \sqrt{\frac{g}{L}}t + \arctan{\left ( \frac{C_1}{C_2} \right )} \right) } \end{align*} }$$
A su vez también se pueden encontrar las siguientes relaciones de las ecuaciones del movimiento en función de la posición.
$${\large \begin{align*} a(t) &= -\frac{g}{L} \cdot r(t) \\ v(t) &= \sqrt{\frac{g}{L}} \cdot \sqrt{L^2 - \|r(t)\|^{2}} \end{align*} }$$
Por último las constantes $C_1$ y $C_2$ de la solución de la ecuación del movimiento pueden hallarse con las condiciones iniciales respectivas del sistema.
Movimiento del péndulo simple con unas respectivas condiciones iniciales
Si se tiene las condiciones iniciales siguientes para el movimiento del péndulo simple de longitud L = 1m
Condiciones Iniciales del movimiento de péndulo simple lineal en t = 0
- $\theta(0) = 15^{\circ}$
- $w(0)$ = 0 rad/s
 |
| Simulación del Péndulo Simple Lineal |
Condiciones Iniciales del movimiento de péndulo simple no lineal en t = 0
- $\theta(0) = 162^{\circ}$
- $w(0)$ = 0 rad/s
 |
| Simulación del Péndulo Simple no Lineal |
Comentarios
Publicar un comentario