Introducción
Luego de que Newton desarrollara sus leyes de la mecánica clásica, habían ciertos problemas que no podían resolverse considerando a la materia como una masa puntual (partícula).
Algunos problemas relacionados a esto eran los fenómenos ondulatorios de la materia tales como la luz en la óptica, el efecto doppler entre otros. Por tanto para analizar y comprender todos los fenómenos de carácter ondulatorio, entender la fuerza de Lorentz y la luz. Maxwell después del aporte de físicos anteriores como Faraday y Ampere como también matemáticos anteriores como Gauss. Maxwell propuso su teoría electromagnética de la cuál inicialmente presento 20 ecuaciones, sin embargo luego se sintetizaron en 4 ecuaciones que poco después fueron conocidas como las leyes de Maxwell.
En esta pequeña entrada detallaremos lo que son las ecuaciones de Maxwell y su relación que tiene que ver con la física clásica de Newton y la física relativista de Einstein.
Marco Teórico
Como se menciono en la introducción las ecuaciones de Maxwell, es decir, la teoría electromagnética de Maxwell surgió con el fin de explicar el carácter ondulatorio de la materia.
Las ecuaciones de Maxwell son de importancia debido a que hizo posible la existencia de la teoría de la relatividad, ya que Einstein decidió dar validez a esta teoría antes que la teoría de Newton en lo que se refiere a la velocidad de la luz en el vacío.
La teoría electromagnética de Maxwell afirma que una onda de luz tiene una velocidad constante mientras que la mecánica de newton afirma que se tienen que cumplir las transformaciones galileanas de la velocidad para todo marco de referencia inercial, sin embargo estas dos teorías no podían entenderse correctamente.
Si realizamos las transformaciones de galileo para una dimensión se puede observar lo siguiene:
- Sin transformación de Galileo, x' = x. $${\large \begin{equation}\frac{\partial^2\vec{E}}{\partial x'^2} = \frac{1}{c^2}\frac{\partial^2\vec{E}}{\partial t^2} \hspace{2cm} ... (1)\end{equation}}$$
- Con transformaciones de Galileo, x' = x - vt.$${\large \begin{equation}\frac{\partial^2\vec{E}}{\partial x'^2} + \frac{1}{v^2}\frac{\partial^2\vec{E}}{\partial t^2} + \frac{2}{v}\frac{\partial^2\vec{E}}{\partial t\partial x'}= \frac{1}{c^2}\frac{\partial^2\vec{E}}{\partial t^2} \hspace{2cm} ... (2) \end{equation}}$$
Donde se puede apreciar claramente que las ecuaciones (1) y (2) no son iguales. Por tanto las transformaciones de galileo no son compatibles en la teoría electromagnética de Maxwell.
Las ecuaciones de Maxwell para la física clásica están dadas por las siguientes ecuaciones en su forma diferencial e integral:
 |
| Leyes de Maxwell en su forma diferencial e integral |
Ley de Gauss para la Electricidad:
Esta ley explica que si hay una carga eléctrica dentro de una superficie cerrada entonces el flujo eléctrico es proporcional a la carga eléctrica por el inverso del coeficiente de permeabilidad eléctrica en el vacío o también que la divergencia del campo eléctrico es proporcional a la densidad de la carga eléctrica por el inverso del coeficiente de permeabilidad eléctrica en el vacío.
Ley de Gauss para el Magnetismo:
Esta ley explica la no existencia de los monopolos magnéticos, es decir, las líneas del campo magnético siempre son cerradas lo que quiere decir que no atraviesan a la superficie en la cual se encuentran. Por tanto se deduce que el campo magnético no diverge por tanto es igual a cero.
Ley de Faraday - Lenz:
Esta ley explica que una diferencia de potencial eléctrico es proporcional al negativo de la rapidez del cambio del flujo magnético que atraviesa una bobina respectiva. A este fenómeno se le conoce como también inducción electromagnética debido a que se puede obtener corriente a partir de un campo magnético, a su vez la diferencia potencial será mayor con el número de espiras de la bobina.
Ley de Ampére - Maxwell:
Esta ley explica que la circulación del campo magnético no estacionario a través de una curva es producida y es proporcional a una corriente eléctrica que se desplaza por un flujo eléctrico que varia con respecto al tiempo. Esta ley es la análoga de la ley de Faraday - Lenz ya que explica que usando una corriente eléctrica se puede obtener un campo magnético respectivo.
Estas 4 ecuaciones anteriores explican completamente los fenómenos con respecto al electromagnetismo. Fue el gran trabajo de James Clerk Maxwell quién ideo esta teoría luego de revisar el trabajo de Michael Faraday y sus ideas con respecto a los campos. A lo que le llevo a introducir de manera rigurosa el concepto de campo electromagnético y la fuerza que actúa sobre ellas "La fuerza de Lorentz" que es igual a :
$${\large \begin{equation*} \vec{F} = q( \vec{E} + \vec{v} \times \vec{B}) \end{equation*} }$$
Se debe recalcar que la fuerza de Lorentz no cumple la tercera ley de newton, debido a que las fuerza de Lorentz no es colineal, es decir, cambia de dirección en todo momento.
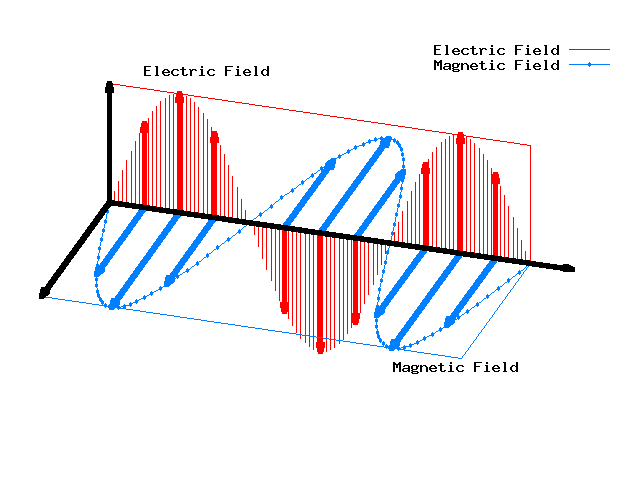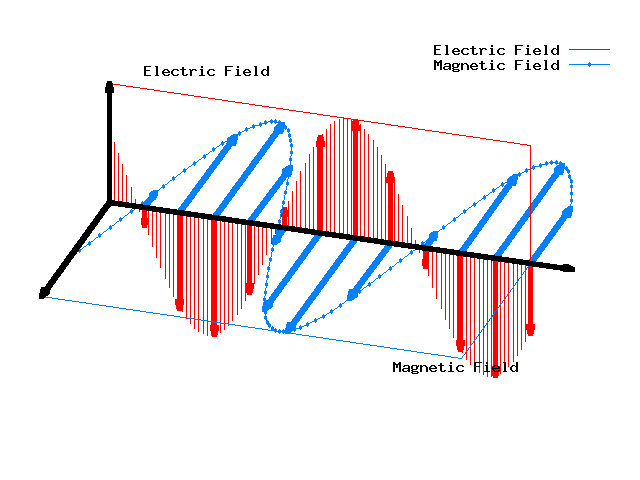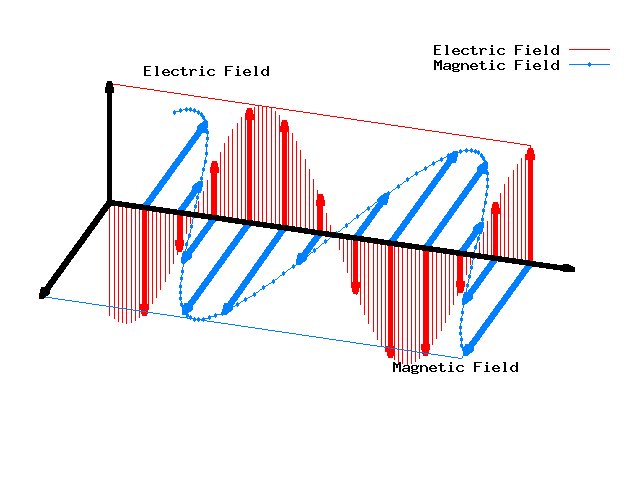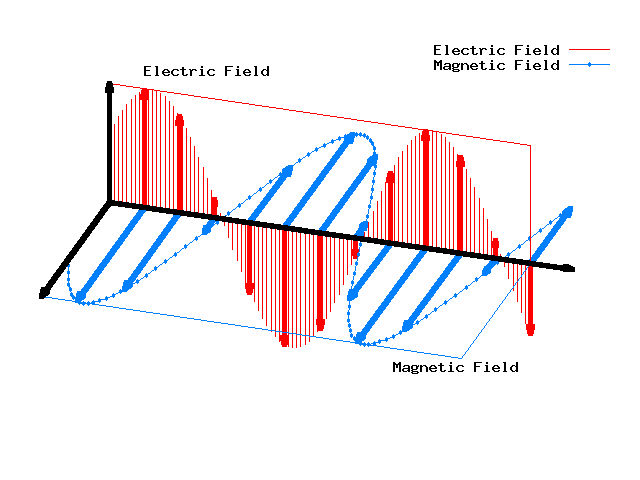
A su vez la teoría electromagnética de Maxwell predijo la existencia de ondas electromagnéticas y su respectiva velocidad probada experimentalmente por Hertz, una de ellas fue la luz la cuál se encuentra en el espectro visible.
Las ecuaciones de Maxwell pueden reducirse a dos ecuaciones de onda una para el campo eléctrico y otra para el campo magnético las cuales son las siguientes:
$${\large \begin{equation*} \triangledown^2 \vec{E} = \frac{1}{c^2}\frac{\partial^2\vec{E}}{\partial t^2} \hspace{1cm}, \hspace{1cm} \triangledown^2 \vec{B} = \frac{1}{c^2}\frac{\partial^2\vec{B}}{\partial t^2} \end{equation*} }$$
No obstante si aplicamos el principio de superposición de las ondas para las ondas lineales podemos unir las ecuaciones de onda del campo magnético y campo eléctrico en una sola onda la cuál es la onda electromagnética.
$${\large \begin{equation*} \triangledown^2 (\vec{E} + \vec{B}) = \frac{1}{c^2}\frac{\partial^2(\vec{E} + \vec{B})}{\partial t^2} \end{equation*} }$$
Donde:
la constante c = ${\large \begin{equation} \frac{1}{\sqrt{\varepsilon_{0}\mu_{0}}} \end{equation} }$ es igual a la velocidad de la luz.
La ecuación de onda electromagnética esta clasificada:
- Onda tridimensional porque su frente de ondas se da en tres dimensiones
- Onda transversal porque la propagación es perpendicular a la dirección de propagación
- Onda periódica porque luego de un tiempo T llamado periodo la onda cumple un ciclo.
La onda Electromagnética explica muchos fenómenos ondulatorios que tienen que ver con la luz como también explican muchas de sus propiedades tales como los fenómenos ópticos de reflexión y refracción, el espectro electromagnético, la radiación de cuerpo negro, etc.
La teoría electromagnética de Maxwell fue la que uso Einstein como base para poder desarrollar la teoría de la relatividad especial debido a que dio validez a la afirmación de que una onda de luz siempre tiene una velocidad constante "Experimento de Michelson - Morley", experimento que demostró la no existencia del eter y la contracción del tiempo y la longitud.
Aunque Einstein nunca tuvo conocimiento del "Experimento de Michelson - Morley". Este experimento fue necesario para probar que las ideas que tenia eran correctas y que la falla era la mecánica de Newton, ya que al aplicar las transformaciones de galileo a la ecuación de onda de Maxwell, ecuaciones (1) y (2) no daban los resultados que se esperaban respectivamente.
Está discrepancia se debía al considerar que el tiempo era absoluto, es decir había simultaneidad en los fenómenos físicos para todos los observadores de los sistemas inerciales. Idea que fue predominante antes del aporte de Einstein, sin embargo ahora sabemos con los experimentos que no es válida.
Ya con la entrada de la teoría de la relatividad especial de Albert Einstein, se tuvo que cambiar de las transformaciones galileanas a las transformaciones de Lorentz para la velocidad en los distintos marcos de referencia inerciales. A continuación las transformaciones de Lorentz para una dimensión
$${\large \begin{equation*} x' = \frac{x - vt}{\sqrt{1 - \frac{v^2}{c^2}}} \hspace{0.5cm}, \hspace{0.5cm} y' = y \hspace{0.5cm},\hspace{0.5cm} z' = z \hspace{0.5cm}, \hspace{0.5cm} t' = \frac{t - \frac{vx}{c^2}}{\sqrt{1 - \frac{v^2}{c^2}}} \end{equation*} }$$
Donde:
- c es la velocidad de la luz
- t' es el tiempo que miden los demás observadores en S(x,y,z,t)
- $\frac{1}{\sqrt{1 - \frac{v^2}{c^2}}}$ es la contracción de Lorentz
Curiosamente las ecuaciones de maxwell eran invariantes bajo este tipo de nuevas transformaciones lo que le daba validez a la teoría electromagnética. Los únicos cambios sustanciales que se tuvo que hacer con las ecuaciones de maxwell fueron simplemente colocar a las magnitudes físicas en cuadrivectores o en notación tensorial. La inclusión del potencial vector del cual los campos eléctrico y magnético pueden formarse en función de está nueva magnitud física. A su vez se pueden deducirse de las ecuaciones de Maxwell.
$${\large \begin{align*} \vec{E} &= - \triangledown \phi - \frac{\partial A}{\partial t} \\ \vec{B} &= \triangledown \times \vec{A} \end{align*}}$$
El potencial vector se puede expresar en cuadrivectores y esta dada por la siguiente ecuación
$${\large \begin{equation*} A^{\mu} = \left( \frac{\phi}{c} , A\right) \hspace{1cm},\hspace{1cm} \partial _{\mu} A^{\mu} = 0 \end{equation*} }$$
En la relatividad especial también se cumple la conservación de la densidad de carga eléctrica y en notación de cuadrivectores está dada por la siguiente ecuación:
$${\large \begin{equation*} J^{\mu} = \left( c\rho , J \right) \hspace{1cm},\hspace{1cm} \partial _{\mu} J^{\mu} = 0 \end{equation*} }$$
Los valores del campo eléctrico y campo magnético pueden hallarse a partir del potencial vector y pueden visualizarse en el siguiente tensor que se muestra a continuación:
$${\large\begin{align*} F^{\mu\nu} &= \partial^\mu A^\nu - \partial^\nu A^\mu \\ F^{\mu\nu} &= \begin{bmatrix} 0 & - \frac{E_x}{c} & - \frac{E_y}{c} & - \frac{E_z}{c} \\ \frac{E_x}{c} & 0 & - B_z & B_y \\ \frac{E_y}{c} & B_z & 0 & - B_x \\ \frac{E_z}{c} & - B_y & B_x & 0 \end{bmatrix} \end{align*} }$$
Donde:
$${\large \begin{equation*} \partial = \left( \frac{1}{c}\frac{\partial}{\partial t}, \triangledown \right) \end{equation*} }$$
Conclusiones
- Saber cuales son las ecuaciones de Maxwell de la física clásica tanto en su forma diferencial y en su forma integral respectivamente.
- Entender que fenómenos físicos explican las ecuaciones de Maxwell y cuál es su relación correspondiente con la luz y sus respectivas características ondulatorias.
- Entender las incompatibilidades entre la mecánica clásica de Newton y el electromagnetismo de Maxwell antes de la aparición de la relatividad especial de Einstein.
- Dar una breve descripción del electromagnetismo en la relatividad especial y porque las ecuaciones del electromagnetismo son invariantes en la relatividad especial.
- Las diferencias entre las transformaciones de Galileo y las transformaciones de Lorentz para el electromagnetismo en los sistemas de referencia inerciales.
Comentarios
Publicar un comentario